Journals
Biomechanical Study of Simulated Metastatic Peri-Acetabular Defects
A B S T R A C T
Peri-acetabular metastasis presents the risk of fracture. However, the relationship between bone loss and fracture risk is unknown. Utilizing fresh frozen intact cadaver pelves, Harrington class I lesions were simulated. Lesions were categorized as small (< 40%) or large (> 40%) Axial loading was applied in a quasi-static mechanism by a mechanical testing system to catastrophic failure, with the load-to-failure force being measured. There was statistical difference in the load-to-failure force between hemi-pelves with large defects and their matched controls. It was found that mean load-to-failure strength of a hemi-pelvis with a Class I defect was more than 2.3-2.45 times the calculated hip joint reactive force. Thus, it was concluded that a pelvis with a peri-acetabular defect of greater than 40% has a significantly lower load-to-failure strength compared to an intact pelvis. However, even this large Class I defect will fracture only at supra-physiologic loads and the hip joint may not normally be exposed to forces that high.
Keywords
Peri-acetabular, Harrington, biomechanical
Abbreviations
Musculoskeletal Transplant Foundation (MTF), poly-methylmethacrylate (PMMA), body weight (BW).
I N T R O D U C T I O N
Metastatic bone disease is a common ailment referred to the orthopaedic oncologist. The pelvis represents one of the most common sites of metastasis second only to the spine [1, 2]. A review done by Picci et al. showed that at one institute, 18.8% of 4431 archived bone metastases occurred in the pelvic region [3]. As metastatic defects increase in size, the relative bone strength decreases lending to pathologic fractures as a common impending complication. Additionally, the risk of pathologic fracture may also be tied to the amount of force, or loading force, placed on the defect. Thus, involvement of weight-bearing structures such as the pelvis, and more specifically the acetabulum, pose an increased risk of pathologic fractures [4]. In the event pelvic fractures occur, they may cause significant pain for patients, debilitating injuries, and ultimately reduced quality of life [5]. While cure is often not attainable for patients with metastatic lesions to the bone, the potential for complications necessitates the need to evaluate for surgical intervention prior to complications [4-6].
The pelvis in conjunction with the sacrum facilitates the transfer of weight from the upper body to the hips. Depending on the activity, forces as high as 5.5 times body weight may be transferred from the femur to the acetabulum, with the major portion of the load transferred through the cortical shell [7-9]. Previously, finite element models have explored load distribution of the hip during normal daily activities such as walking. By deconstructing the movements of walking, including walking upstairs, force distribution throughout the hip may be investigated. Studies have shown the stresses in cortical bone to be about 50 times higher than those of underlying trabecular bone, with the highest stresses occurring in the superior acetabular wall during the single leg stance [9]. Given this, it follows that fractures or any cortical defect in this region may impede with critical daily activities, making their prevention ever more important.
Surgical intervention with acetabular involvement poses a unique challenge to surgeons due to the region’s complex anatomy and proximity to neurovascular structures [10]. There have been several reports on the treatment of metastatic acetabular lesions, most of which employ the Harrington Classification System [4]. Based on this classification system, defects are categorized into one of four categories depending on the extent of pelvic involvement and treated accordingly (Table 1). Despite management of these various stages being previously studied, there remains a lack of a reliable data demonstrating the indication for surgical management in relation to the amount of bone loss and the risk of pathologic fracture [5, 10, 11].
Our proposed study aims to derive data that will help predict the interconnection between lesions and fracture risk in metastatic acetabular lesions. Class I lesions simulated in hemi-pelvis cadaver specimens were subjected to quasi-static loading forces. Force was applied to these specimens as well as their non-defect matched pairs to catastrophic levels, allowing fracture to occur. Our hypothesis is that contained defects within the peri-acetabular bone without cortical destruction do not significantly increase the risk of fracture.
Table 1: The Harrington Classification
|
Class |
Defect |
Treatment |
|
1 |
Peri-acetabular lesion with intact cortices |
Radiotherapy vs. cemented THA |
|
2 |
Medial wall defect |
Protrusio cage with cemented THA |
|
3 |
Deficient lateral, superior, medial walls |
Harrington reconstruction with Steinman pin fixation and protrusion cage/cemented THA |
|
4 |
Isolated lesion |
En bloc excision for cure |
Experimental Design
Lesion Simulation
Eight (8) fresh frozen intact cadaver pelves and their associated proximal femora were obtained from the Musculoskeletal Transplant Foundation (MTF). Harrington Class I lesions were simulated by making 1 cm2 cortical perforation in the supra-acetabular region using a tube saw and manually curetting out cancellous bone in the peri-acetabular area (Figure 1). The volume of the defects created was measured utilizing three-dimensional reconstruction of the hemi-pelvis with standard axial computed tomography images (GE Light Speed Plus). From a true lateral view of the hemi-pelvis, a line adjoining the top of the greater sciatic notch and the anterior inferior iliac spine was drawn, and axial images reconstructed parallel to this line. This reference line served to control for the pelvic tilt in each specimen. Axial images were taken at one-millimeter increments and the area of the defect and the intact bone measured on each axial cut. By summing the defect areas versus the total bone area excluding the cortical bone, defect volumes are reported as a percentage of the entire ilium volume. This in turn normalized the peri-acetabular volumes because the pelvic specimens are of different sizes (Figure 2). Eight (8) fresh frozen intact cadaver pelves and their associated proximal femora were obtained from the Musculoskeletal Transplant Foundation (MTF). Harrington Class I lesions were simulated by making 1 cm2 cortical perforation in the supra-acetabular region using a tube saw and manually curetting out cancellous bone in the peri-acetabular area (Figure 1). The volume of the defects created was measured utilizing three-dimensional reconstruction of the hemi-pelvis with standard axial computed tomography images (GE Light Speed Plus). From a true lateral view of the hemi-pelvis, a line adjoining the top of the greater sciatic notch and the anterior inferior iliac spine was drawn, and axial images reconstructed parallel to this line. This reference line served to control for the pelvic tilt in each specimen. Axial images were taken at one-millimeter increments and the area of the defect and the intact bone measured on each axial cut. By summing the defect areas versus the total bone area excluding the cortical bone, defect volumes are reported as a percentage of the entire ilium volume. This in turn normalized the peri-acetabular volumes because the pelvic specimens are of different sizes (Figure 2).
Figure 1: X-ray of Simulated Class 1 defect
Sample Preparation
The hemi-pelves were mounted on a servo-hydraulic mechanical testing system (MTS Systems Corp., Minneapolis, MN) in the following orientation: in the lateral view, the ASIS and pubic tubercles are vertically aligned; in the AP view, the femoral shaft is adducted 150 relatives to the horizontally level pelvis. Following the technique described by Levine et al, each hemi-pelvis was potted via the sacroiliac (SI) joint in poly-methylmethacrylate (PMMA) and re-inforced by wood screws [12]. The symphyseal body was stabilized with a bolt connected to the mounting construct. The femur and acetabulum were then rotated as a unit by 150 to approximate the angle of the resultant joint reaction force vector during normal walking; the proximal femur was potted on the loading platform with PMMA, at a level 4 cm distal to the lesser trochanter (Figure 3) [13]. Thus, when axial loading was applied to this construct, the force vector applied to the hip joint simulated the vector of the joint reaction force during the single-leg stance phase of walking.
Figure 2: Method of volume calculation
Figure 3: Loading Apparatus
Mechanical Testing
For the mechanical testing, the cortical perforation was covered with a thin layer of bone cement. Axial loading was applied in a quasi-static mechanism by a mechanical testing system (MTS) to catastrophic failure at a rate of 20mm/min (Figure 3) as described by Levine et al. [12]. The load to failure force was measured in Newtons and the location of failure was noted (Table 2). The mean load-to-failure was analyzed for the whole group, as well as for lesions less than 40% volume (small defect) and lesions more that 40% volume (large defect).
Statistics
Statistical analysis was performed using a student’s t-test using p < 0.05 to evaluate for significant differences in the load-failure rates between defected hemi-pelves versus their matched controls, as well as between large and small defects.
Results
Of the eight matched hemi-pelves utilized in this study, five were considered to have small lesions and three large lesions. When subjected to catastrophic loading forces, all but one of the pelves (specimen 1) failed. All three specimens in the large defect group failed in the peri-acetabular area, while only one of four specimens in the small defect group failed in the peri-acetabular region (Table 2). There was no significant difference in the load-failure between controls (M = 5589.38, SD = 2239.21) and defects (M = 4486.5, SD = 2130.6) for the study as a whole; t (14) =1.0092, p= 0.33. There was no statistical difference between hemi-pelves with small defects (M = 4231.6, SD = 2774.94) and their matched controls (M = 4936.8, SD = 2622.91); t (8) = 0.4130, p = 0.6905. There was statistical difference between hemi-pelves with large defects (M = 4911.3, SD = 233.14) and their matched controls (M = 6677.0, SD = 975.12); t (4) = 3.0503, p = 0.0380. Specifically, our results suggest that only large defects (>40%) cause a significant risk of pathologic fractures compared to intact pelves.
Table 2: Results
|
Specimen |
% Lesion volume (Cancellous) |
Load to Failure (N) (Control) |
Load to Failure (N) (Defect) |
Location of Failure (Control) |
Location of Failure (Defect) |
|
1 |
18.9% |
8989 |
9089 |
No failure |
No failure |
|
2 |
31.7% |
1760 |
2105 |
Iliac wing |
Proximal femur |
|
3 |
34.5% |
4516 |
3663 |
Femur fracture |
Iliac wing |
|
4 |
34.9% |
5312 |
3042 |
Iliac wing |
Superior Dome |
|
5 |
34.9% |
4107 |
3259 |
Iliac wing |
Iliac wing |
|
6 |
43.8% |
6025 |
5171 |
Iliac wing |
Superior Dome |
|
7 |
44.2% |
7798 |
4720 |
Proximal femur |
Superior Dome |
|
8 |
45% |
6208 |
4843 |
Iliac wing |
Superior Dome |
Discussion
The present study aims to help predict the interconnection between lesions and fracture risk in metastatic acetabular lesions. Quasi-static loading forces were applied to Class I lesions simulated in hemi-pelvis cadaver specimens. Catastrophic loading forces were applied and measured, allowing for the risk of pathologic fracture to be assessed. Pelvic bone metastases continue to be a concern of the orthopaedic surgeon, as reduced structural integrity of diseased bone continues to raise concerns of pathologic fractures. Previously, the risk of pathologic fracture has been proven to depend on the location of the lesion, bone properties, as well as force of loading [14]. In a study of nine different daily living activities which were assumed to cause high hip joint load, no forces or moments were more critical than during fast walking or stair climbing, with the exception of stumbling where forces of up to 870% body weight (BW) were in play [8]. The average peak force during normal walking at 4 km/hr was between 211 and 285 % BW. The highest (compressive) normal stress occurs during the one-legged stance of the walking cycle with the loads mainly transferred from the acetabulum through the lateral cortical shell to the SI joint and the pubic symphysis [13, 15]. While it is uncommon in the everyday life of a cancer patient for the hip joint to be subjected to catastrophic loading, stumbling remains an exception. Given the distribution of force, it holds that maintaining acetabular structure, as well as cortical structure, is imperative in decreasing fracture incidence.
To the author’s knowledge, the present study is the first of its kind. Previously, distribution of force through pelvic anatomy has been studied in finite element models [16-25].These studies have largely focused on quantity and distribution of forces in specific positions, such as sitting or walking, and their relation to safety, comfort, disease processes, as well as treatment. By investigating the connection between extent of metastatic lesions and pathologic fracture risk, our hope was to expand on current knowledge as well as help guide whether or not prophylaxic surgical intervention is warranted for class I defects. Based on our results, only large defects resulted in increased risk of fracture, requiring an average of 6677 N to do so. Even so, the fact remains that this quantity of force is unlikely to be encountered by a cancer patient during normal daily living activities. Previously, a biomechanical study by Bergmann et al. demonstrated hip joint reactive forces in two patients during walking, jogging, and stumbling [8]. There was one male and one female subject in the study, weighing 650 N and 470 N respectively. They were able to show hip reactive forces to be the greatest during stumbling, peaking at about 870% body weight (BW). Even so, the hip joint reactive force remained between 280% BW and 480% BW depending on the speed at which the patient was walking. Utilizing this data, the expected joint reactive force was calculated for our cadaver specimens. It was found that mean load-to-failure strength of a hemi-pelvis with a Class I defect was more than 2.3-2.45 times the calculated hip joint reactive force. Thus, it was concluded that a pelvis with a peri-acetabular defect of greater than 40% has a significantly lower load-to-failure strength compared to an intact pelvis. However, even this large Class I defect will fracture only at supra-physiologic loads and the hip joint may not normally be exposed to forces that high.
The results of this study warrant the discussion of whether current industry standards for the management of Class I lesions need to be change. Given the surgical complexity of peri-acetabular fixation, the benefit of doing so must be carefully weighed against the risk of pathologic fracture. In the author’s opinions, volumetric measurements of lesions via CT-scanning should be conducted as part of pre-operative evaluation. In the event lesions are found to comprise ≤40% of peri-acetabular structure, and cortices are intact, it is advisable to forgo prophylaxic fixation. Further evaluation of large (>50%) lesions to determine whether they cause clinically relevant pathologic fractures remains to need further investigation.
Figure 4: Graph of Mean Load-to-Failure Strengths and Calculated Joint Reactive Force
Article Info
Article Type
Research ArticlePublication history
Received: Tue 16, Oct 2018Accepted: Mon 05, Nov 2018
Published: Sat 29, Dec 2018
Copyright
© 2023 Jennifer Thomson. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. Hosting by Science Repository.DOI: 10.31487/j.JSO.2018.01.003
Author Info
Francis R. Patterson Jennifer Thomson Joseph Benevenia Kathleen S. Beebe Michael N. Kang
Corresponding Author
Jennifer ThomsonRutgers New Jersey Medical School Department of Orthopaedics, NJ
Figures & Tables
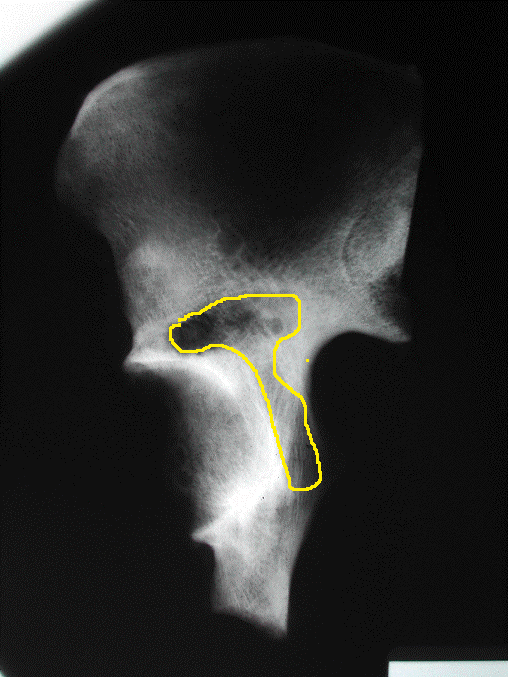



Table 1: The Harrington Classification
|
Class |
Defect |
Treatment |
|
1 |
Peri-acetabular lesion with intact cortices |
Radiotherapy vs. cemented THA |
|
2 |
Medial wall defect |
Protrusio cage with cemented THA |
|
3 |
Deficient lateral, superior, medial walls |
Harrington reconstruction with Steinman pin fixation and protrusion cage/cemented THA |
|
4 |
Isolated lesion |
En bloc excision for cure |
Table 2: Results
|
Specimen |
% Lesion volume (Cancellous) |
Load to Failure (N) (Control) |
Load to Failure (N) (Defect) |
Location of Failure (Control) |
Location of Failure (Defect) |
|
1 |
18.9% |
8989 |
9089 |
No failure |
No failure |
|
2 |
31.7% |
1760 |
2105 |
Iliac wing |
Proximal femur |
|
3 |
34.5% |
4516 |
3663 |
Femur fracture |
Iliac wing |
|
4 |
34.9% |
5312 |
3042 |
Iliac wing |
Superior Dome |
|
5 |
34.9% |
4107 |
3259 |
Iliac wing |
Iliac wing |
|
6 |
43.8% |
6025 |
5171 |
Iliac wing |
Superior Dome |
|
7 |
44.2% |
7798 |
4720 |
Proximal femur |
Superior Dome |
|
8 |
45% |
6208 |
4843 |
Iliac wing |
Superior Dome |
References
1. Ham SJ, Schraffordt Koops H, Veth RP, van Horn JR, Molenaar WM, et al. (1998) Limb salvage surgery for primary bone sarcoma of the lower extremities: long-term consequences of endoprosthetic reconstructions. Ann Surg Oncol 5: 423-436. [Crossref]
2. Unwin PS, Cannon SR, Grimer RJ, Kemp HB, Sneath RS, et al. (1996) Aseptic loosening in cemented custom-made prosthetic replacements for bone tumours of the lower limb. J Bone Joint Surg Br 78: 5-13. [Crossref]
3. Picci P, M.M., Fabbri N, Gambarotti M, Vanel D (2014) Atlas of Musculoskeletal Tumors and Tumorlike Lesions. Springer.
4. Harrington KD (1981) The management of acetabular insufficiency secondary to metastatic malignant disease. J Bone Joint Surg Am 63: 653-664. [Crossref]
5. Muller DA, R Capanna (2015) The surgical treatment of pelvic bone metastases. Adv Orthop 2015: 525363.
6. Quinn RH, Randall RL, Benevenia J, Berven SH, Raskin KA (2013) Contemporary management of metastatic bone disease: tips and tools of the trade for general practitioners. J Bone Joint Surg Am 95: 1887-1895. [Crossref]
7. Bergmann G, Graichen F, Rohlmann A (1993) Hip joint loading during walking and running, measured in two patients. J Biomech 26: 969-990. [Crossref]
8. Bergmann G, Deuretzbacher G, Heller M, Graichen F, Rohlmann A, et al. (2001) Hip contact forces and gait patterns from routine activities. J Biomech 34: 859-871. [Crossref]
9. Dalstra M, Huiskes R, van Erning L (1995) Development and validation of a three-dimensional finite element model of the pelvic bone. J Biomech Eng 117: 272-278. [Crossref]
10. Kiatisevi P, Sukunthanak B, Pakpianpairoj C, Liupolvanish P (2015) Functional outcome and complications following reconstruction for Harrington class II and III periacetabular metastasis. World J Surg Oncol 13: 4. [Crossref]
11. Benevenia J, Cyran FP, Biermann JS, Patterson FR, Leeson MC (2004) Treatment of advanced metastatic lesions of the acetabulum using the saddle prosthesis. Clin Orthop Relat Res 426: 23-31. [Crossref]
12. Levine RG, Renard R, Behrens FF, Tornetta P (2002) Biomechanical consequences of secondary congruence after both-column acetabular fracture. J Orthop Trauma 16: 87-91. [Crossref]
13. Dalstra M, Huiskes R (1995) Load transfer across the pelvic bone. J Biomech 28: 715-724. [Crossref]
14. Hipp JA, McBroom RJ, Cheal EJ, Hayes WC (1989) Structural Consequences of Endosteal Metastatic Lesions in Long Bones. J Orthop Res 7: 828-837. [Crossref]
15. Bay BK, Hamel AJ, Olson SA, Sharkey NA (1997) Statically equivalent load and support conditions produce different hip joint contact pressures and periacetabular strains. J Biomech 30: 193-196. [Crossref]
16. Martins JA, Pato MP, Pires EB, Jorge RM, Parente M, et al. (2007) Finite element studies of the deformation of the pelvic floor. Ann N Y Acad Sci 1101: 316-334. [Crossref]
17. Phillips AT, Pankaj P, Howie CR, Usmani AS, Simpson AH (2007) Finite element modelling of the pelvis: inclusion of muscular and ligamentous boundary conditions. Med Eng Phys 29: 739-748. [Crossref]
18. Shim VB, Pitto RP, Streicher RM, Hunter PJ, Anderson IA (2007) The use of sparse CT datasets for auto-generating accurate FE models of the femur and pelvis. J Biomech 40: 26-35. [Crossref]
19. Anderson AE, Peters CL, Tuttle BD, Weiss JA (2005) A Subject Specific Finite Element Model of the Pelivs: Development, Validation and Sensitivity Studies. J Biomech Eng 127: 364-373. [Crossref]
20. Bai X, W.G, et al. (2010) Finite Element Musculloskeletal Modeling of Mechanical Virtual Human of China.
21. Cheng Z, S.J, et al. (2007) Considerations and Experiences in Developing a Finite element Buttock Model for Seating Comfort Analysis.
22. El-Asfoury MS, E.-H.M (2009) Static and Dynamic Three-Dimensional Finite Element Analysis of Pelvic Bone. International Journal of Mathematical, Physical and Engineering Sciences.
23. Kim SH, P.J, et al. (2010) Digital human Body Model for Seat Comfort Simulation. International Journal of Automotive Technology 2010: 239-244.
24. Vezin P, V.J (2005) Development of a Set of Numerical Human Models for Safety.
25. Silvestri C, R.M (2009) Development of a Finite Element Model of the Knee-Thigh-Hip of a 50th Percentile Male Including Ligaments and Muscles. International Journal of Crashworthiness 14: 215-229.
